Quantum Teleportation

Quantum Teleportation

Without using a quantum channel, how can we transfer qubits?

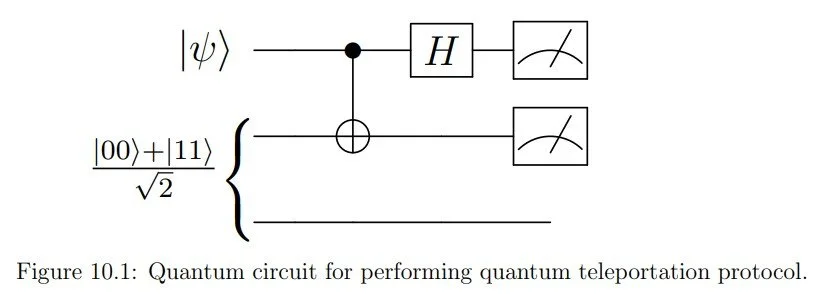
Let’s say Alice and Bob share an entangled pair and a classical channel. The standard solution to this problem is illustrated in the diagram below.

Alice owns qubits 1 & 2, and wishes to send the first. Qubits 2 & 3 comprise the standard bell pair, which is maximally entangled. Let's express the target qubit ψ in the standard basis with arbitrary amplitudes.

Initially, the qubits are in the state:

After the CNOT gate, the state is:

After the Hadamard gate, the state is:

Alice measures her qubits in the standard {|0>, |1>} basis, which gives 4 possible outcomes. Each outcome leaves Bob’s qubit in a determined state. By sending 2 bits of information, Alice can tell Bob which state Bob’s qubit is currently in. Subsequently, Bob can correct his qubit by performing at most 2 operations, like so:

As such, when Alice sends 2 classical bits, if the first is 1, Bob should apply the Z gate. If the second bit is 1, Bob should apply the X gate. If a bit is 0, he doesn’t apply the corresponding gate. Doing so will restore the target qubit ψ!

Does this allow for instantaneous qubit transfer? Wouldn’t that violate Special Relativity?

Recall that this protocol requires Alice to send a classical bit to Bob, which is restrained by the speed of light.

Where is ψ after Alice measures, but before Bob performs his operation?

The answer is that ψ is shared between Alice and Bob, but neither can access it alone. It’s as if they’ve both put a private lock on a shared “chest” (psi).